TRIZ/USIT
Paper: 
USIT
Operators for Solution Generation in TRIZ: Clearer Guide to
Solution Paths
held at Florence, Italy,
on Nov. 3-5, 2004 (Proceedings, pp. 347-363)
| TRIZ/USIT
Paper: |
|
|
USIT
Operators for Solution Generation in TRIZ: Clearer Guide to
Solution Paths
|
|
| Toru Nakagawa (Osaka Gakuin University, Japan) | |
| ETRIA
World Conference: "TRIZ Future 2004", held at Florence, Italy, on Nov. 3-5, 2004 (Proceedings, pp. 347-363) |
|
| [Posted
here on Nov. 16, 2004] [Japanese
translation version posted on Oct. 18, 2004] |
|
buttons.
Editor's Note
(Toru Nakagawa, Nov. 15, 2004)
The
ETRIA
"TRIZ Future 2004" Conference was held in Florence, Italy two weeks
ago. The conference was a much success with 125 participants in
total coming from 22 countries. I am going to write a Personal
Report of the Conference, as I did for these 6 years, but it will only
be
ready to post here after 3 weeks or so. Thus I have decided to
post my paper now separately from the report. I wish to thank Dr.
Gaetano Cascini and the staff of University of Florence for their
efforts for making the Conference so successful.
"Why
the
penetration of TRIZ has been slow in the Western (industrial) world?"
has been a major concern inside the current TRIZ community.
Victor
Fey, in the keynote speech of the ETRIA Conference 2004, said: "TRIZ is
good. Distribution of TRIZ is bad. Don't touch
TRIZ!". A number of researchers argued against it, giving
different observations on the reasons and proposing/demonstrating
different approaches of teaching/applying/distributing TRIZ.
I
have been
working to make the problem solving method in TRIZ simpler and yet
effective to learn and to apply by using the framework of
USIT. It was my understanding till half a year ago that the
main weak point in TRIZ was the lack of clear
(not-too-complex) overall procedure of problem solving in TRIZ and that
this was caused by the separation of pairs of analysis and
solution-generation methods (i.e. principal solution methods request
their own analysis methods).
The
present
paper is a further extension of my series of works. My new
understanding described here is that the weak point of TRIZ is its lack
in a clear 'overall
structure' in the problem solving. Notice that an overall
procedure can be represented with a flowchart while an overall
structure can best be illustrated with a 'data-flow diagram', where
information required/obtained in each step are shown in
boxes. Overall structure of TRIZ and of USIT are compared
in the present paper (see Figs. 2 and 4 respecitively). An new
scheme of problem solving structure (Fig. 8) is now proposed clearly on
the basis of USIT. The new scheme gives us a clear guide to
solution paths, to follow in a logical and yet creative manner.
Thus USIT is a new generation of TRIZ, being simple, unified, and
effective.
Contents:
2. Current Scheme of Problem Solving
in TRIZ
2.1 TRIZ Knowledge Bases of Principles and Facts
2.2 Individual Methods and Techniques for Problem
Solving in TRIZ
2.3 Overall Procedure of Problem Solving in TRIZ
3. Unified Structure Inventive
Thinking (UST) as a Simple and Unified TRIZ
3.1 Main Features of USIT
3.2 Problem Solving Procedure in USIT
3.3 Overall Structure of Problem Solving in USIT
4. USIT Solution Generation Operators
4.1 The Hierarchical System of USIT Solution Generation Operators
4.2 Illustration of Applying USIT Operators in a
Simple Case: Picture Hanging-Kit Problem
4.3 Guidelines of the USIT Solution Generation
Operators
4.4 Experiences of Teaching and Applying USIT
| Page top |
Paper
top |
1.
Introduction |
2.
Scheme in TRIZ |
3. USIT |
4. USIT Operators |
5. Conclusion |
References |
Nakagawa
et
al. Reorganizing TRIZ into USIT |
Japanese
page |
Abstract
1.
Introduction
Theory of Inventive Problem Solving
(TRIZ) [1, 7, 9, 2] is
a powerful methodology for creatively solving problems in a wide range
of technological (and many other non-technological) fields. It
has established knowledge bases (KBs) of technological facts with
various useful indexing systems and of principles for inventive
thinking and has also developed a large number of methods for problem
definition, problem analysis, and solution generation. These KBs
have been constructed by extracting world best solutions in science and
technology, and the problem solving principles in TRIZ are at a high
level of abstraction so as to be applicable to a wide range of problems.
In spite of
expectations by TRIZ experts,
however, TRIZ has not been spreading so widely and rapidly in the
Western countries since its exposure in early 1990s. The present
author [3] observes, as
many would agree, that the penetration of TRIZ has been slow not
because it is poor but because it is so rich in contents. 'How to
choose an effective principle' and 'how to apply a principle properly
to the user's specific problem' have been the issues for TRIZ
users. Most TRIZ specialists have tried to teach the rich
contents of TRIZ KBs and thinking methods in more or less orthodox
forms, but most engineers in industries and engineering students cannot
understand them up to the level being able to apply them to their real
problems. Some specialists may say 'It is a problem of the
students and the training period', but the position of the present
author in this paper is 'It is a problem of the teachers and the system
of TRIZ itself.'
Basic model and
overall structure of TRIZ
should be reviewed and discussed in this context. It is generally
understood that TRIZ is based on the four-box
scheme of problem solving
[2] shown in Fig. 1. Instead of trying to solve user's
specific problem directly to specific solutions staying at the concrete
level, TRIZ advises to go around at a higher abstraction level using
standard models which show generalized problems and their generalized
solutions. TRIZ has adopted this scheme from the sound basis of
science and technology.
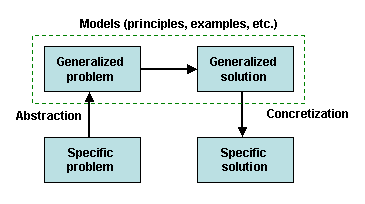
All the TRIZ KBs (such as Effect database, Inventive Principles,
Inventive Standards, Trends of Evolution, etc.) have been built with
the intention to let them serve as different models at the abstract
level in this scheme.
Once models are established, the process of problem solving may be reduced to the following issues:
Generally speaking,
these issues are not
well understood unfortunately in many fields of science and
technology. In each topic of a specialty field, one model is
chosen and taught with a few examples. Then the students have to
learn, study, drill and practice many times to understand by themselves
that the model is useful for some kind of problems after some kind of
abstraction.
TRIZ has developed a
number of procedural
methods of problem solving in technology, for the purpose of guiding us
in the abstraction and selection (and little in the concretization)
processes. These methods in TRIZ (such as 9-Window Method,
Substance-Field Analysis, Technical and Physical Contradictions, etc.)
are often very unique and powerful in the areas where no other
effective methods and ways of thinking exist. Nevertheless, the
overall procedure of problem solving in TRIZ has not been well
established yet and is in a confusing situation for users.
In the present
paper, the current
situation of the TRIZ methodology is summarized briefly in this
four-box scheme. Then I will demonstrate that Unified Structured Inventive Thinking (USIT) [8], i.e. a simplified and
unified version of TRIZ, has established a clear structure of problem
solving procedure by extending the four-box scheme into more meaningful
six-box scheme. The key to this structure is the USIT Solution
Generation Operators, which have been obtained earlier by reorganizing
all the TRIZ principles and methods for solution generation [4, 5].
2. Current Scheme of
Problem Solving in TRIZ
The current situation of the overall
scheme of problem solving in TRIZ may be roughly summarized as
shown in Figure 2 in the framework of Figure 1. TRIZ KBs are
shown in a box at the top and various TRIZ methods are shown in ovals
according to the phases in problem solving. These components are
established well [1, 7, 9, 2]
and are summarized in the following subsections first and the overall
structure will be discussed next.
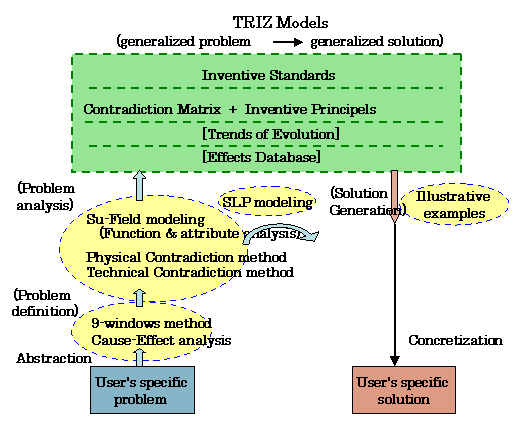
2.1 TRIZ
Knowledge Bases of Principles and Facts
First type of KBs in TRIZ
is the accumulation of facts and technical means, especially:
This type of KB is
useful to learn
various facts and means known in different fields of science and
technology and to apply them to our own fields in novel ways.
Reorganizing the KB in the explicit hierarchical system of functions
has been a major contribution of TRIZ.
Second type of KBs in TRIZ is at a higher level of abstraction of the principles for inventive thinking and has been the most important contribution of TRIZ. They include:
These are the major
models in TRIZ in the
four-box scheme and provide problem solvers with generalized solutions
for generalized problems. For each item in these KBs, examples of
typical cases of application are accumulated and linked (e.g., to the
Effects Database and to patent databases) and used for illustrating and
stimulating users' analogical thinking. It should be noted that
these KBs are presented to users as parallel alternatives, separated
(and more or less overlapped) with one another, as shown with the
separating broken lines in Figure 2.
2.2 Individual
Methods and Techniques for Problem Solving in TRIZ
In the area of methods and techniques for problem solving in
technology, Classical TRIZ has
developed a number of unique and effective methods. Major ones
are summarized below briefly with particular comments on their
relationships to the TRIZ KBs:
2.3
Overall Procedure of Problem Solving in TRIZ
The above description of the components of TRIZ KBs and TRIZ
methods and their positions shown in Figure 2 are basically agreed in
the community of TRIZ specialists
[1, 7, 9, 2]. The overall
procedure of problem solving in TRIZ must further specify the
recommendation of 'which methods and which KBs should be used in which
order in which situation of problem.' This is the issue on which
many TRIZ leaders have proposed and applied in many different ways, and
is still under a confusing situation as follows:
Altshuller [1] who developed all the
individual methods and KBs in Classical TRIZ also developed the overall
procedure in the name of ARIZ
(Algorithm of Inventive Problem Solving). Intending to
make ARIZ more and more powerful for solving ever harder problems, he
constructed various versions of ARIZ having complicated procedure of
using various individual methods and their corresponding KBs. He
recommended to use ARIZ after at least 80 hours of training, and for
solving simpler problems he advised to use more standard methods (i.e.,
some appropriate individual methods).
Yuri Salamatov, in
his orthodox TRIZ
textbook [7], recommends
to try several inddividual methods listed above and use ARIZ later only
when no satisfactory solutions are obtained. Boris Zlotin and
Alla Zusman [9] have
proposed TRIZ Tool Map and recommended to use different individual
tools depending on the type of sub-problems which are suggested by the
cause-effect analysis.
Darrell Mann in his
recent textbook [2]
proposes a four-stage
process composed of 'define the problem', 'select the solution tool',
'solve the problem', and 'evaluate the solution' stages. Though
his explanation of individual methods is excellent and insightful, his
overall process seems to contain two problems: Methods for
problem analysis, i.e. the main part of the abstraction process in the
four-box scheme, are described separately in the 'problem definition'
and the 'problem solving' stages. In the 'tool selection' stage,
he shows 19 situations of judging the results of the 'problem
definition' stage and recommends for each situation up to four tools to
select in the 'problem solution' stage. The selection table is
too large and complicated to summarize here.
Thus these overall procedures of problem solving in the traditional TRIZ have in common the following weak points:
3.
Unified Structured Inventive
Thinking (USIT) as a Simple and Unified TRIZ
USIT is a simplified and unified version of TRIZ, having reorganized
all the TRIZ methods for problem analysis and solution generation,
having constructed a clear full procedure for problem solving, and
having a clear scheme of problem solving.
3.1 Main
features of USIT
USIT was developed by Ed Sickafus [8] at Ford Motor Co. in 1995
by adopting and enhancing Israeli Systematic Inventive Thinking (SIT),
which was a much simplified method of TRIZ developed in early
1980s. USIT has the following features:
The present author [3-6] introduced USIT into Japan since 1999 and further refined it. The main features of refinement are:
3.2
Problem Solving Procedure in USIT
The whole procedure in USIT is expressed in the flowchart [3] as shown in Figure
3. Problem solving in USIT is done in three distinguished phases,
i.e., problem definition, problem analysis, and solution
generation. In the problem analysis phase, we have three
principal methods, i.e., (a) the Function and Attribute Analysis of the
current system, (b) the Particles Method for considering an ideal
solution first, and (c) Space and Time Characteristics Analysis.
Using either (a) or (b) depending on the nature of the problem is all
right, but using both (a) and (b) for any problem is highly recommended
from recent practices. Sequential use of (a), (c), and (b) is the
typical current practice. In the solution generation phase, the
five USIT operators are applied repeatedly onto possible operands in
the system or in the solution space.
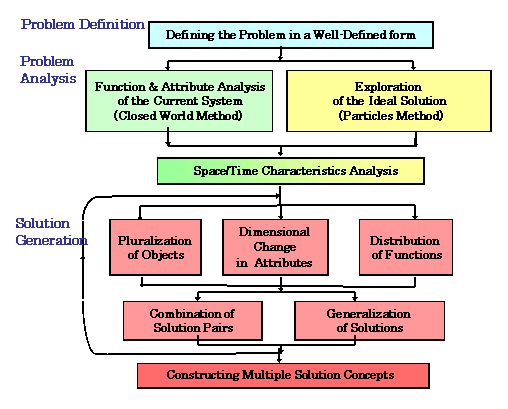
The flowchart representation of USIT has been used since the initial
days of USIT development. It is quite natural because the group
work of problem solving in USIT is actually conducted in sessions
following this flowchart. Typically, Session 1 for the problem
definition phase, Sessions 2 and 3 for the problem analysis phase using
the methods (a)+(c) and (b), respectively, and Sessions 4 and 5 for the
solution generation phase.
3.3 Overall
Structure of Problem Solving in USIT
Now let us consider
to map the USIT
process onto the basic four-box scheme of problem solving shown in
Figure 1. It is important to notice that the four boxes represent
not the processes (or methods) but the information (or data) and that
the arrows represent the processes. Thus we are going to draw, in
terms of information science, a 'dataflow
diagram' of problem solving in USIT:
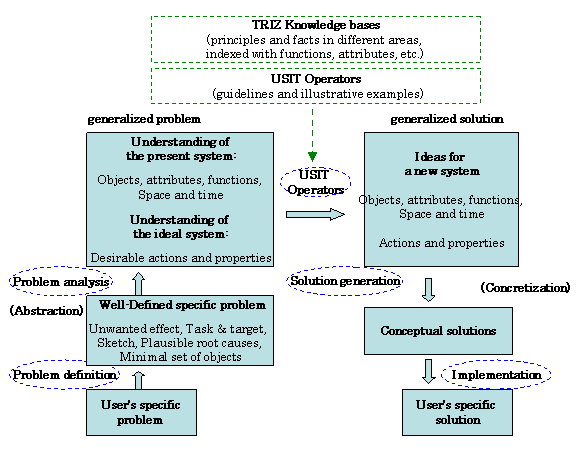
This dataflow
diagram (Figure 4) of the problem
solving process in USIT demonstrates (and claims) the following points:
4. USIT
Solution Generation Operators
4.1 The
hierarchical System of USIT Solution Generation Operators
The USIT Solution Generation
Operators [5]
form a hierarchical system as shown in Figure 5. There are 5
principal operators which may be further classified into 32
sub-operators in total.
4.2
Illustration of Applying USIT Operators in a Simple Case: Picture
Hanging-Kit Problem
Before discussing the nature of the USIT Solution Generation
Operators, we better have some illustrative examples in a simple case
study [6]. Let me
use the Picture Hanging-Kit Problem [8]. Our task is 'To
improve the ordinary picture hanging-kit composed of a nail, a string,
and two hooks so that the picture is not apt to tilt'. Let us
skip the description of the processes of problem definition and problem
analysis (see Ref. [8, 3, 6]).
As the generalized problem model
in this case, we have the following pieces of information among others.
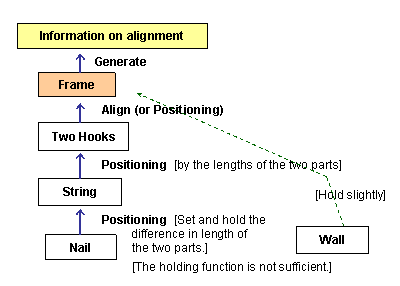
Focusing on the nail, for example, let
us apply various USIT Operators. A part of such
application results are demonstrated in Figure 7.
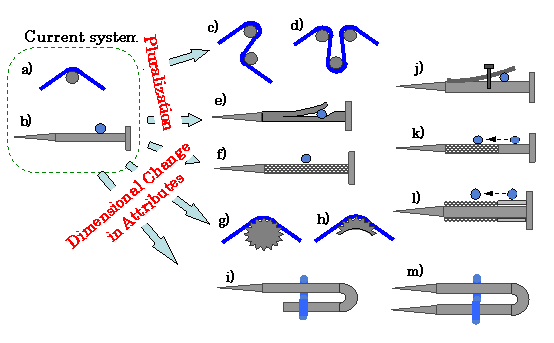
Figures a) and b) show the original nail with a string. The
'Multiply' operator (1b) is the simplest case of Object Pluralization (1), and gives
solutions c) and d) with the intention of increasing the
friction. 'Division' (1c) is also a form of Pluralization, and
gives an idea shown in e) with the intention of holding the string
tightly at the narrow slit. If we want tighter holding function
after adjustment, we may attach a screw as shown in j).
The second principal
operator advises 'Dimensional Change
in Attribute',
and f) is a simple response where the smoothness attribute of the nail
surface is changed into a much different value, i.e. making the nail
surface rough. Since rough surface is not good for adjusting, we
have an idea shown in k) where only half of the nail is made rough
whereas the other half is left smooth; this guides us the idea of
adjusting the string at the smooth part of the nail and holding the
string at the rough part. The idea l) is to use a collar having
rough and smooth parts around the nail body. The surface of
the nail may be changed not just rough but rugged, suggesting to change
in the cross-sectional shape as shown in g). Since only the top
part of the cross-section is actually used, we may change the
cross-sectional shape and size more drastically as shown in h).
The operational idea of 'changing shape' of the nail gives us another
solution shown in i), which effectively has two nail bodies. When
I noticed that the nail i) is apt to be turned by the string tension,
the idea of two-footed nail m) came up. This may be regarded as
the result of 'Unify' operator (1d) applied on the two nails shown in
c).
You may notice in the above explanation that other 3 principal USIT operators have not appeared explicitly. But don't worry. Many of the above solutions are explainable as the results of other USIT operators as well. For example, the idea k) can be explained to have been obtained in different ways as follows:
In this manner,
different USIT operators
sometimes (or often) guide us to the same conceptual ideas. This
shows the intended redundancy
in the USIT solution generation operators.
For obtaining an
idea, these operators
may and may not be in mind explicitly beforehand. But it should
be noticed that the reflection of any ideas in the general terms of
these operators is important for understanding
the solutions in its essence. For example, among the five
ways of interpreting the idea k), the interpretation with the 'Operator
(4c): Combination in time' is found to be most essential in this
problem. This operator, in its essence, corresponds to the
application of the strategy of Separation in time to a Physical
Contradiction, in the orthodox TRIZ terms. Thus recognizing the
idea k) in terms of this Operator of 'Combination in time' can lead the
user to recognize the Physical Contradiction at the core of this
problem and its possible elimination with the Separation in Time.
With this understanding, the user will be able to generate many more
novel solutions easily.
4.3 Guidelines
of the USIT Solution Generation Operators
The USIT Operators for solution generation have their guidelines (i.e., brief instruction
accompanied by a schematic diagram) at the 32 sub-operator level and at
even more detailed levels. They reflect various TRIZ principles
and have been reformulated in a much useful way [4, 5]. By way of
example, let us discuss about the 'Divide
an object' operator (1c) in USIT. This operator has been
derived from several TRIZ principles including:
In deriving the USIT guidelines from TRIZ principles, we have chosen the following stand points:
Thus the guideline
for the USIT Operator (1c) is described as follows:
Some more
examples of guidelines in USIT are shown for other four
operators which appear in the previous subsection:
From these examples
of guidelines in
USIT, I hope the readers understand that a number of TRIZ principles
(including Inventive Principles, Inventive Standard, Trends of
Evolution, etc.) are smoothly unified in these USIT Operators, and that
the solution examples shown above are easily obtainable by applying
these USIT Operator guidelines.
Usefulness and
intended redundancy of
USIT Operators are based on the USIT concepts of Objects, Attributes,
and Functions. The USIT Operators on Objects (as shown in case of
(1c)) take some Objects as the operand, apply the specified operation
on the Objects, and then further apply modifications onto Attributes
and Functions of the operand Objects according to the guideline
descriptions. Situations are similar in the USIT Operators on
Attributes and on Functions. This type of extension in the USIT
guideline descriptions guides the problem solver in a way easier to
follow than most TRIZ principles. At the same time, the
mentioning of Objects, Attributes, and Functions in each guideline
description is the source of intended redundancy, i.e. overlapping, of
the USIT Operators.
4.4
Experiences of Teaching and Applying USIT
Experiences of teaching and applying USIT in Japan have been
reported in [3, 6].
A lecture of 2 hours can cover the overview of TRIZ and USIT.
Typically, two-day USIT training
seminar is held in a company with 15-25 participants of
engineers. After the overview lecture, 3 real industrial problems
are brought in by the participants and are tried to solve in parallel
group practice following the USIT procedure. 5 sessions are
carried out, where each session is composed of a short lecture of the
process, parallel group practice, and presentation &
discussion. Usually each group generates 20 to 40 ideas which may
be further concentrated into several conceptual solutions worthy of
further consideration for implementation. Thus engineers, who
were novice of TRIZ/USIT, can have the experience of solving an
industrial problem with USIT by themselves, and can understand the full
USIT procedure with 3 real case studies. This shows the easiness
and effectiveness of learning USIT in comparison with learning
TRIZ.
5.
Concluding Remarks
In the basic four-box scheme of problem solving, generalized models of
TRIZ (and many other scientific/technological theories) are expressed
by the generalized problems and their corresponding generalized
solutions, and are supposed to be used with analogical thinking.
Abstraction is for mapping the user's specific problem to the
generalized one in the model, while concretization is for mapping
backwards. These mapping processes, however, are often not well
explained in the procedural manner.
The present paper
proposes a different scheme of
problem solving, as
summarized in Figure 8.
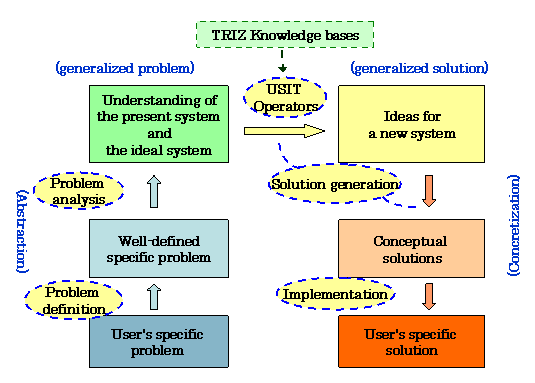
Abstraction is done in two
steps; the problem definition step converts the user's specific but
often vague problem into a well defined specific problem and the
problem analysis step converts it further into the abstract
understanding of the current and ideal systems. This abstract
understanding of the system is expressed in the basic terms of objects,
attributes, functions, space, time, desirable actions, and desirable
properties, etc. and is in place of the generalized problem of the
four-box scheme. Then the Solution
Generation Operators in USIT transform the elements of the
abstract system into modified elements of a new solution system; this
is the key step in the whole problem solving. Then conceptual solutions are formed on
the basis of technological thinking, and finally user's specific
solutions may be designed in technology.
It should be noticed
that the vagueness
in the analogical thinking disappear in the new scheme. Knowledge
expressed in the 'Models' in TRIZ (and problem solving methods in
general) has been concentrated into the USIT Operators. And hence
all the procedures of creative problem solving are now expressed in
much clearer terms and procedures.
This unification
and simplification of TRIZ can help people understand TRIZ more
easily and widely and apply TRIZ to their real problems, as
demonstrated earlier.
References
& J ).]; Jan.
2002 (J).; Sept. 2002 (J). ; Sept. 2002 (J).;
Jan. 2003 (J). & J ).]
| Page top |
Paper
top |
1.
Introduction |
2.
Scheme in TRIZ |
3. USIT |
4. USIT Operators |
5. Conclusion |
References |
Nakagawa
et
al. Reorganizing TRIZ into USIT |
Japanese
page |
Last updated on Nov. 16, 2004. Access point: Editor: nakagawa@utc.osaka-gu.ac.jp