TRIZ Textbooks:  CID Course for Children, 2-2G01
Introductory Lesson  Methods of Solving Problems  Topic 1.  “We wouldn’t be happy if misery didn’t help us”      (Contradictions)
Fantasy City: Course of Creative Imagination Development (CID),  2nd Grade, 2nd Semester, Methodical Guide-Book
Natalia V. Rubina, 1999 [published in Russian] English translation by Irina Dolina, May 4, 2001 Technical Editing by Toru Nakagawa, Sept. 3, 2001
Posted in this "TRIZ Home Page in Japan" in English on Sept. 11, 2001 under the permission of the Author. (C) N.V. Rubina, I. Dolina, and T. Nakagawa 2001

CID Course Top

Guide-Book Top

0. Introductory Lesson

Topic 1 Contradiction, Lesson 1

Topic 1  Lesson 2

Next Chapter

Workbook of this chapter

Workbook

1.  Warming-up

      “Card index to the CID lessons for the second grade, part 2”

3.  Introduction to the lesson

     “The history of mankind started with an invention.  First stone instruments of labor were devised and first man, homo sapiens, a man of reason appeared on Earth…  It’s difficult to enumerate how many inventions have been made since then.  Everything that surrounds us had to be invented.  For example, we don’t know who invented a sail; this wonderful invention has been living for thousands years.  And it will go on living: there are projects of space ships with sun sails, absorbing the light pressure.  Can you imagine what an inventor felt when he was setting a sail for the fist time?  Probably, it was a sunny and windy day.  A rush of wind filled the roughly made mat and a sail, a raft left the shore.  The first in the history of mankind mast creaked, bending.  Patches of sunlight were dancing on the waves, but the man didn’t notice them.  His heart was beating madly: he was not sure where he would manage to reach the shore again.  He was scared to look back, but all the same – there was a shocking, crazy, great moment of victory!  The wind was obeying the man for the first time, the raft was racing forward, splitting the wave noisily …”  (“And Suddenly the Inventor Appeared”, G. Altov, Moscow, ”Detskaya Literatura”, 1984, p.126.)

4.  Main topic

     So, inventions surround us everywhere.  Let’s go along the streets of Fantasy City and look around through the eyes of an inventor.
 

     At the first lesson on topic “Methods of solving problems” it is very important to use knowledge and experience, that the children have acquired at the CID lessons.  I’ll remind you of the fact that while practicing the methods of making images, we paid attention to the positive and negative consequences of the changes in systems.  “Technical systems, like living bodies, consist of interconnected parts.  If “for no reason” we enlarge one part of the system, this will have a negative impact on its other parts.  That is why the inventive problems always contain two requirements: it is necessary to improve some part (some property) of a system and at the same time not to deteriorate its other parts (other properties) or all the system as a whole.  To make an invention means to overcome a technical contradiction.” (G. Altov: “And Suddenly the Inventor Appeared”, Moscow, “Detskaya Literatura”, 1989, p. 15.)
     The properties of the systems manifest themselves in the interaction with other systems.  In any interaction there are pluses and minuses. Plus means that the property of a system meets the requirements of a super-system; minus means that the same property contradicts the requirements of another super-system. To solve a problem means to eliminate minus, preserving plus.  (Fulfilling these tasks, in which it is necessary to find systems that are big and small, slow and fast at the same time, we have already tried to combine opposite properties.  In the problem about “a big hospital in a small town” the hospital itself is big, but the separate parts are small.  The vacation can be slow in winter and fast – in summer).  Our task is to learn how to reveal pluses and minuses in a system, where the problem emerged.  In other words, to learn to reveal contradictions.  We are familiar already with some methods of solving contradictions: to assemble – to disassemble, to do upside down, to divide in time. The talk about the methods and rules of solving contradictions is ahead.
“The problem and the answer” are two banks of the river.  An attempt to guess the answer at once is like an attempt to jump from one bank to the other.  The technical contradictions and the  methods form a bridge. The theory of solving inventive problems is , actually, a science about building unseen bridges, over which the thought moves towards the new ideas.
     However, the contradictions and methods seem more correctly to be compared with the bridge piers.  To jump from a pier to a pier is not easy: one needs a guess-work to turn from the problem to the contradiction and from the contradiction to the method.  Besides the piers the beams, connecting the piers, are needed – then we’ll have a good bridge, over which we can quietly and confidently, step by step come to from the problem to the answer.
We’ll talk about such a bridge later.  Meanwhile one thing is important: an inventor has to reveal and to overcome the technical contradictions.  This simple idea is the beginning of the theory of solving inventive problems”.
         (G. Altov “And Suddenly the  Inventor Appeaed”. Moscow, “Detskaya Literatura”, 1989, p.17.)

     Let’s try to figure it out.  It is necessary that the traffic lights should be seen.  In summer the branches hide the traffic light.  It is possible, of course, to cut the branches, but they will grow again.  Usually the procedure is as follows: The traffic light pole is replaced.  What should be done to make the traffic lights be seen well, even if the pole not to be replaced at all?   Let’s articulate it another words.
     If the traffic light pole is replaced often, the lights will be seen well (+), but it takes much time (–).
     We need the pole, that can change its size and its shape, and we don’t have to replace it often.  Have you imagined such a pole?   What does it look like?

     Write down your answer.
          _______________________________________________________
 

     It was proposed to make the pole that can fold like an accordion: it can be easily increased and decreased, curved and it doesn’t need to be replaced often.

     And now, draw your attention to the definition, that helped us to find the correct answer.  Let’s write down this definition, taking away everything that refers to the concrete problem.
 

   This definition of the Contradiction helps to see the essence of a problem, i.e., the most important thing in the problem under consideration. To solve the problem means to solve the contradiction.  In other words, it is necessary to preserve (+) and remove (–).

Problem 2.  In a Latin American country the government noticed that the merchants were concealing their profits.  To increase taxes, it seemed ineffective to reinforce punishments.  All the merchants were given the same forms of the bills to fill in when they sold any product.  But they began to sell goods, without writing the bills (the customers didn’t need the copies of the bills and didn’t ask for them).  What should be done?

If………………………………………………………………….,
then (+)……………………………………………………………,
but (–)……………………………………………………………

     If the merchants are forced to write out the bills, the real profits will be revealed (+), but it won’t be effective (–).
     The customers can help us by demanding the copies of the bills.
     The administration announced the lottery of the numbers on the bills.  The customers began to demand the copies of the bills from the merchants.

Problem 3.  In the presence of the police it is necessary to distribute the invitations to the secret seminar.  What should be done not to attract the attention of the policemen?

If………………………………………………………………….,
then (+)……………………………………………………………,
but (–)……………………………………………………………

     If the invitations are distributed secretly only to the seminar participants, then (+) the seminar will be attended only the people that are wanted, but (–) the policemen might suspect something wrong.
     The distribution of the invitations shouldn’t arouse suspicion of the police.
     The invitations were given to everybody: the policemen got invitations to the concert, the secret society members got invitations to the seminar.

7.  Sum up

     “The inventions, including the process of creating, testing, and implementing, are always connected with the fascinating adventures.  The victory over a new technical problem needs a flexible mind and courage not less than those that d’Artagnian needed to fight the crafty designs of the Cardinal Rishilieau…  However, the inventory problems sometimes are stronger and more cunning than any cardinals.  If you want adventures, modern, clever, and useful to people, invent!  The fascinating adventures, that will last your whole life, are waiting for you in the sphere of technical creativity.  But you have to prepare yourself for these adventures, beginning from childhood; the earlier, the better, as in sports.  So, don’t waste your time…
     I wish you success!”
     (“And Suddenly the  Inventor Appeared”, G. Altov, Moscow, “Detskaya Literatura”, 1984, p.126.

    Homework:  Watch the city life, your life, and find contradictions, arising around you.  Write down your observations on the cards in the end of your exercise book.
 

Workbook

Lesson 1.

1.  Warm up

     “Card index to the CID lessons for the second grade, part 2”.

2.  Homework

     What contradictions did you manage to find?

  This task has an interesting psycho-correcting peculiarity.  The children often suggest contradictions that are the reflections of their own worries.  If a child articulates the contradiction, singles out the problem, he will have a real possibility to solve it.

3.  Introduction to the lesson

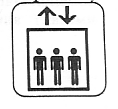
Problem 4 .  The accident in an elevator.  Four people got stuck there.  Three of them are upset, one is happy.  Who is he?

Let’s make a chart:
 
 

 

	+	–
A student with high grades
A student with low grades
A teacher

     Direct the thoughts of the children against the psychological inertia.  This can be, for example, a kid, who was playing “hide and seek”, or other games and who hid in this stuck elevator.  Ask them to think about other circumstances, when one needs to hide safely for a while.

4.  Main topic

     So, the same incident may be considered to be good and bad.  All depends on a super-system, in which it happens.
 

     This lesson is a continuation of the talk about contradictions.  Articulating of the contradictions is one of the main and strongest instruments of TRIZ.  The contradictions, articulated correctly, lead to the solution of a problem.  In order to see and articulate the contradictions correctly, the systematic activities are necessary.  The best of such activities is solving school creative problems first together with a teacher, then independently.  Here arises a rather commonplace problem, facing the adults in the course of TRIZ education.  In the beginning, in particular, while solving low-level problems, it seems easier to sort out possible variants.  Besides, the well-known “national trait of a Russian” – the keenness of wit can really helps to solve such problems.  However, if you are enough patient and insistent, you will notice that articulating the contradictions becomes gradually the natural part of your students thinking.

5.  Psycho-technical and developing games
 

Three piglets live in Fantasy City.
Nif-Nif is a cheerful piglet;
Naf-Naf is a grumbling piglet;
Nuf-Nuf is a clever piglet.

     Three piglets like to play a game, called “Good – Bad”.  The rules of the game are rather simple.  A situation is offered, you have to explain what is bad and what is good there.
 

     For this game the class is divided into two groups.  The first group acts on behalf of  Nif-Nif and suggests some solutions of the arising contradictions.  The second group, acting on behalf of Nuf-Nuf,  reveals what is bad.  From time to time Nuf-Nuf shows up and offers some solutions of arising contradictions.

4.  Main topic (continuation)

     In order to learn how to devise an invention, it is important to see (+) and (–) of any incident, and to remove (–), preserving (+).

Activity 1.  We can change systems with the help of the methods of image making.  Let’s look at these changes through the inventor’s eyes:

- choose a system;
- apply any method of image making;
- what is good and what is bad in this change.

     The system approach referring the methods of making images was very precisely described in the work of I. N. Murashkowska ”When I become a wizard”:
     " “Once in Shanghai I saw a Chinese with the ears so large that they served him as a pelerine.  When the rain started, the Chinese would cover himself with his ears and he was fine: dry and warm.  If he met his friends during the rain, he would cover them with his ears.  Then they would sit together and sing their sad songs, until the rain stopped.”  This is one of the stories, that Peppy Long Stocking used to tell her friends.  Let the kids give their ideas how to use large ears.
     It might turn out that they can not devise any interesting solutions.  Then, what?   Why do they fail?
     ... let’s see what the system approach to the work of such type can offer us.
      We notice that the problem arises because of the change of a system – the ears  have become large.  We have to find an application for them, to define positive consequences of this change.  We know that the change of a system itself doesn’t cause consequences.  The consequences arise as a result of interaction of the systems.  It means that we need to see the possible super-systems, the situations, in which this Chinese is involved.  We will find out with whom and with what he interacts there.  Only after that  we will be able to determine the consequences.
     Let’s single out typical situations for any person: sleep, washing-up, morning exercises, eating, having a walk, rest, sports, communication, trips, family events, encounters with friends and so on.  And untypical situation: dancing on a camel back, living under the water, driving the clouds away, hiding the cities, etc. – anything that comes to mind.
     Let’s choose a situation – for example, eating, - and add things that are also included in this super-system: a table, a plate, rice, chop sticks, other eaters, smells, air, etc.
     The ears are so large that they will hang down on the table and it will be good because they can be used as plates.  Or if the rice falls down, it can be caught with the help of the ears and put into the mouth – then the chopsticks are not needed.  Some people like kitchen smells, some people don’t; the ears can drive the smells away, directing them to those who appreciate it.  Uncovered food cools quicker, the ears can keep it warm.”
     I. N. Murashkowska: “When I become a wizard”, Selection “Poznanie”, Riga, 1993.

     Now we deal with the most interesting things.  Let’s try to use our knowledge about contradictions for solving the problems.
     Take your time while sorting out variants.  Find a contradiction in the problem.

Problem 6.  In the end of the last century some interesting attraction was being demonstrated in the circuses around Europe: an elephant that could count, add up, subtract, multiply and divide within the limits of 100.  There was a screen on the arena, with the numbers from 1 to 100, distinctly written on it.  The elephant took the pointer with his trunk and pointed out the correct answer to the question, asked by the audience.  Guess the clue to this trick.

If………………………………………………………………….,
then (+)……………………………………………………………,
but (–)……………………………………………………………

     If an elephant can really count, then (+) the trick is solved, but (–) it is impossible to train an elephant to count.
     To specify this contradiction, let’s single out a system, where the problem has appeared.  It consists of the elements: an elephant, a pointer, and a screen.
     If an elephant is trained to hold the pointer with his trunk, (+) he will be able to point at the screen, but (–) the answers will be wrong.
     Is it possible “to train” a pointer, but not an elephant, to show correct answers on the screen?  One of the well-known properties of the iron pointers is to be attracted to a magnet.   We’ll use it to establish the necessary interaction between a pointer and a magnet.
     Indeed, the secret of the trick is in the fact that the screen is equipped with an electromagnet.  An operator behind the curtains switches the cell on the screen, corresponding to the correct answer.  The trainer only has to train the elephant to keep a pointer and to direct it towards the screen.

7.  Sum up

Homework.
Problem 7.   At the toys factory the doll “Carlson“ was being made.  It is common knowledge that Carlson has to fly.  But at this point a contradiction has appeared.  If a small screw is made, Carlson will look like a real character and it will be very convenient to play with him.  But he won’t be able to fly.  If a screw is big, the doll will fly, but it will look like a windmill.  Such a doll can’t even stand on its legs.  What can be done?

If………………………………………………………………….,
then (+)……………………………………………………………,
but (–)……………………………………………………………

     If we make the fans of the screw big, then (+) Carlson will fly, but (–) the toy won’t be convenient to play with.
     If we make the fans of the screw small, then (+) Carlson will be comfortable to play with, but (–) the toy won’t fly.
     Thus, while flying, the fans must be big, while resting they must be small.
     We have already tried to solve such contradictions.  Big and small at the same  time.
     The fans of the screw should be made of thin plates, that can be folded like the toy “tongue”.   When the plates are unfolded and become big, Carlson can fly.

Workbook

1.  Warming-up

“Card index to the CID lessons for the second grade, part 2”

     Discussing the problem about Carlson.

3.  Introduction to the lesson

     Contradiction:  In the north it is getting dark very early.  In order to light up the room, many candles are needed.  If there are many candles, (+) the room is lighted up brightly, but (–) the candles are expensive, they smoke, they burn out quickly.

4.  Main topic

     You will be surprised, but the best solution is an ordinary electric lamp.  We got used to it and even don’t notice, how our life has changed with the appearance of the electric appliances.
     Do you know what contradiction is concealed in such a usual and convenient lamp?  The lamp doesn’t burn itself, it’s only the spiral that burns, it consists of some special staff.  This staff gives light when it is heated, but gradually it evaporates and, unfortunately, is quickly broken.  This is a contradiction: if an electric lamp is heated much, it (+) gives bright light, but (–) it is quickly broken.  What is to be done?
     Solution: day-light luminescent lamps, in which a gas substance is burning instead of solid, metallic spiral.  The gas inside the flask can not evaporate and break, like a spiral.

     All systems develop in the course of arising and solving contradictions.  There are many technical systems around us, in which some contradictions were solved.  A pencil consists of the body and the slate.  The main function of a pencil is to leave traces on the paper.  It performs its function thanks to the properties of the slate – the ability to crumble and to stick to the paper.  Let’s imagine a slate without a body.  The same properties would have caused us a lot of trouble: the slate that is constantly being broken and the hands that are always dirty.  Now the next problem that has been solved within this system.  The drawing, the sketch, made by pencil, sometimes need to be corrected or completely changed.  In this case one of the advantages of a pencil manifests itself: we can easily correct inaccuracy, without altering the whole drawing.  For that purpose we need an eraser that we often leave behind or lose.  How to preserve the useful property of the system “pencil – eraser” - to make changes in the drawing easily, and at the same time, to eliminate the ”bad” property of the sub-system – eraser- to get lost or left behind?  The solution is well known to everybody: a pencil with an attached eraser.  (Look at this device that is applied to solve the contradictions – uniting the systems for performing new functions.  Later we’ll talk about this method in detail at the lessons on topic “Perfection”).  Is there any other way of improving a pencil?  What contradictions, existing in this system today, will be removed in the pencils in the future?
     The next activity is aimed at teaching the kids how to find contradictions, already solved in the technical systems around us.  You may build together with us the chains of developing common articles, that illustrate how the contradictions in these system arise and are solved.  And, may be, we’ll try to predict how these systems will change in the future, which contradictions in them will be solved.

Activity 1
     As you see, the inventions are taking place around us.  Let’s look around  through the eyes of an inventor.  Which contradictions have been solved in the following systems?

 

- a desk; - a book; - scissors;  - a pencil;

- a blackboard; - an eraser; - a pencil-case; - shoes.

7.  Sum up

Homework.
Problem 8.  One of the most fascinating performances demonstrated by the lion’s tamers is when a lion opens his mouth wide and a tamer places his head inside.  This performance is very dangerous because even the most obedient lion remains a beast of prey, no matter how well he was tamed.  How do the tamers manage to demonstrate this trick?

If………………………………………………………………….,
then (+)……………………………………………………………,
but (–)……………………………………………………………

     If to place in a lion’s mouth any object, for example, a stick, which won’t let the jaws close, then (+) a tamer will be protected safely, but (–) the trick won’t be interesting to the audience.
     Something that prevents the jaws from closing should be concealed from the spectators.  In the system, where this problem arose, there are the following resources: the head of a tamer, the mouth of a lion, namely, the tongue, the teeth, the lips, the cheeks.  Which of these resources can be used for solving the problems?
     The secret of the trick is in the fact that a tamer before putting his head inside a lion’ mouth, pulls the lion’s lips on his teeth.  When the lion tries to close his jaws, he scratches his lips with his teeth.

CID Course Top

Guide-Book Top

0. Introductory Lesson

Topic 1 Contradiction, Lesson 1

Topic 1  Lesson 2

Next Chapter

Workbook of this chapter

Home Page	New Information	Introduction to TRIZ	TRIZ References	TRIZ Links
TRIZ News & Activities	TRIZ Software Tools	TRIZ Papers and Tech Reports	TRIZ Forum	Home Page

Last updated on Sept. 11, 2001.     Access point:  Editor: nakagawa@utc.osaka-gu.ac.jp