1997米国機械工学会設計工学技術会議(DETC'97)
1997年 9月14-17日, サクラメント, 米国
[著者の許可を得て, 翻訳し, 本ページに掲載 2000. 3. 8]
[英文ページを掲載 2000. 3.23]
まえがき
(『TRIZホームページ』への和訳掲載にあたって,
中川 徹, 2000. 3. 8)
本論文の出典は以下のとおりである。
Creative Design Methodology and the SIT Method
Roni Horowitz and Oded Maimon (Department of Industrial Engineering, Tel
Aviv University),
Proceedings of DETC'97: 1997 ASME Design Engineering Technical Conference,
September 14-17, 1997, Sacramento, California
本論文を掲載するに至った経過は以下の通りである。編者中川は本ホームページにおいて, TRIZの簡易版であるフォード社のUSIT法(Unified Structured Inventive Thinking) について詳しく紹介してきた。TRIZが膨大な体系と問題解決の方法を持っており, その理解と実践のためには, まずもっと簡単で分かりやすい問題解決の思考法を身に付けることが適当であると考えているためである。このUSITは, 1995年にフォード社のDr. Ed Sickafus が, イスラエルのSIT 法を取り入れて改良・実践してきたものである。そのSIT 法は, 1980年代にGenedy FilkovskyがイスラエルでTRIZを簡易化して作ったものであるとのことであった。
小生は, TRIZおよびUSITの理解を進めていく過程で, やはり, イスラエルのSIT 法について正しく理解しておくことが必要であると考えた。そこで, 1999年12月にMr. Filkovsky に電子メールを出し, ついで, Dr. Sickafusが直接教えを受けたDr. Roni Horowitzに電子メールを出して, SIT 法についての情報提供をお願いした。Dr. Horowitzから返事を得ることができたが, Mr. Filkovsky は1990年ころからTRIZを離れているとのことで返事がなかった。Dr. Horowitzからは, 2,3 の論文と学位論文を送って貰った。それらの資料のうち最も分かりやすく代表的なものがこの論文である。,
本論文は1997年のDETC97国際会議で発表され,
その会議の優秀論文賞を獲得した。著者およびASMEに論文の日本語への翻訳と本ホームページへの掲載の許可を申請し,
著者の許可を得てここに掲載するものである。本件の翻訳と公表に関し, 以下の人々に感謝する。
著者: Dr. Roni Horowitz (Tel-Aviv Univ.)
horowitz@eng.tau.ac.il
Professor Oded Maimon (Tel-Aviv Univ.) maimon@eng.tau.ac.il
学会: The American
Society of Mechanical Engineers (ASME)
本論文は,
非常に明確な論理で書かれている。工学的な問題に対する解決策が「創造的」であるためには,
つぎの二つの条件を同時に満たしていれば十分である。
(a) 解決策が,
問題システムおよびその近傍のオブジェクト以外の (種類の) オブジェクトを新たに持ち込まないこと(
「閉世界条件
(CW) 」)
(b)システムの問題の特性を表す関数が,
増加関数から, 減少関数または不変関数へと変わる必要があること (すなわち「質的変化の必要(QC)の条件」)
これらの条件は非常に窮屈に感じられ,
そんな解決策はそう簡単に見つからないと感じられる。しかし, それを見つけると「創造的な」解決策になるのだという。それを,
認知学的な実験で例証している。また, それを見つける方法を非常にすっきりと,
きちんと, 方法として記述し, 具体例で例証している。その方法をSIT 法と呼んでいる
この論文を読むと, USIT法の「閉世界法」の意味が初めてよく分かる。「閉世界」の中で考えること, 「定性変化グラフ」の考え方が, 分かる。また, アイデア生成の諸技法の使い方も示唆的である。USITがSIT 法の何を取り入れて, 何を改変・改良してきたのかも, すこしずつ分かってくる。TRIZもSIT もUSITも, 技法だから, 柔軟に変化してきているのだ, 動きながら改良されているのだということが分かる。重要なことは, 改良の方向を自覚し, 目標を見定めることである。これらの技法を利用する・適用するわれわれも, このような方向・目標を自覚して, 技法を選択し・改良していくべきであると思う。
大変示唆に富む論文であり, 読者の参考に推薦するものである。
なお, Dr.
Horowitzは, 現在はTel-Aviv大学から出て, イスラエルのマルチメディテア関連企業Compedia社に加わり,
新しく創造性教育のためのマルチメディアのソフトウェア/コンテンツの開発をしているとのことである。
なお, イスラエルには, SIT法をマーケッティングなどの分野に適用してコンサルティングの活動をしているSIT社もある。その他にも多くのSIT専門家がいるようだがまだよくわからない。
| 本ページの先頭 | 論文の先頭 | 2. 十分条件 | 4. 経験的実証 | 5. SIT法のプロセス | 6. SIT法の適用例 |
要約:
本論文が提示するのは, SIT 法 (構造化発明思考法) -- 工学設計における創造的問題解決を強化する構造化された方法 -- である。本方法は 3段階の手順である: すなわち, 問題の再定式化, 一般的な探索戦略の選択, そしてアイデア生成技法の適用である。本法の最も革新的な部分は問題再定式化段階である。与えられた問題は, 客観的に定義されまた経験的に検証された, 創造的解決策の十分条件のセットを適用して変形される。本論文は十分条件, および, その応用を例証する経験的研究について記述する。そののち, SIT 法の全体が教育的な例を添えて提示されている。
キーワード: 認知的設計理論, 革新的設計
1. 序論
発明することは, エジソンが言ったように, 1%のひらめきと, 99% の忍耐である。既存の設計方法は発明することの忍耐の部分, すなわち, ルーチン作業として知られているものを扱う: 知識の組織化, パラメタ最適化, データベース検索, チーム会議, ケースベースド設計, および設計プロセスのその他の要素などである。技術者をその真に創造的なアイデアを生産する過程でいかにサポートできるかという問題は, きわめて少数の研究者によってしか注目されなかった。(いまようやく, その分野は人気を得つつあるが。)
創造的アイデアを定義する方法は沢山ある。Dagupta(94) はその文献の中で約80の異なる方法を数えている。本研究では, われわれは単純で普通の定義を使う: 創造的アイデアはその分野の専門家たちによって創造的とみなされるものをいう。この定義が基礎にしている仮定は, 人々は創造的なアイデアを見るとそれを創造的であると同定できるが, 創造的アイデアを構成する性質のアプリオリなリストを提供することはできないということである。専門家の判断をアイデアの創造性の評価に用いることは, 認知科学における創造性の研究者の間では普通の方法である (Hennessey, Amabile, 88) 。この方法を本研究で開発したSIT 法の実験的評価のために使う。
SIT(Structured Inventive Thinking,構造化発明思考法) は, 創造的アイデアに対する十分条件の理論を基礎にしている(Maimon, Horowitz, 96)。その理論によれば, 「技術的問題の解決策としての一つのアイデアが二つの単純で客観的に定式化された条件を満足すれば, そのアイデアはその分野の専門家たちによって創造的とみなされるであろう。」SIT を使って, 問題解決者は, まず自分の問題を再定式化し, 目標を「解決策を見いだす」ことから「これらの条件を満足する解決策を見いだす」ことに変える。ついで問題解決者は解決策を探索するプロセスに進む。この段階で, 彼/ 彼女は二つの一般的な解決戦略の中の一つを選択し, それぞれの戦略は異なるセットの二つのアイデア生成技法に彼らを導く。
創造性一般の研究はここで開発したものとは異なり, 設計を特に対象としたものではない。汎用の創造性戦略として普通に知られているものには, ブレーンストーミング (Osborn, 59), モルフォロジー分析(Morphological Analysis, Allen, 62) , ラテラル思考(Lateral Thinking, de Bono, 92),およびシネクティクス (Synectics, Gordon, 61)がある。主要な違いは, われわれが使う構造化方法論およびわれわれが得る結果にある。
SIT の開発を触発したのはTRIZ (Altshuller 85; Fey, Rivin, Vertkin, 94; Sushkov, Mars, 95; Malmqvist, Axelsson, Johansson, 96)である。TRIZは工学における創造的問題解決を強化するための数少ない方法の一つである。著者たちはTRIZ法を約10年前に知り, それ以来, 100 以上のコースやセミナーをイスラエル, 米国, シンガポールで行ってきた。最初はTRIZ法を教えた。徐々に, 経験に基づく数えきれない修正のサイクルを通じて, また, 理論的・実験的な研究を通じて, その方法は変化し, いまわれわれがSIT と呼ぶ異なった方法になったのである。
TRIZは旧ソビエト連邦において, Genrich Altshullerによって開発された。Altshullerは何千という発明と特許を調べ, それらから, 創造的解決策を特徴づけるいくつかの性質を抽出した。彼が見いだしたことの主要点は, 問題状態中の対立(矛盾)の解消が, 創造的解決策の中に組み込まれているということである。対立とは, なんらかの利益を得るために一つのパラメタを変えなければならないが, それを変えると, 他の重要なパラメタを悪くしてしまうという状態をいう。ルーチン的な工学が対立状況を扱うときには, 最良の妥協点を探す, あるいは, それらのパラメタが取ることができる異なる値の間のトレードオフを求める。
Altshullerが見いだしたのは, 工学的対立を, 関与するパラメタの型によって索引づけできることである。 (39の普遍的な工学パラメタが定義された。) 膨大な数の発明を調査して, それぞれの対立に対して, 問題解決にどうアプローチすべきかのヒントや戦略の候補の組を指定することができた。三つの型のヒントが使われた。原理 (principles),スタンダード(standards),および物理的効果 (physical effects) である。原理 (40の原理がある) は問題を解決する高レベルの戦略である。スタンダード (70のスタンダードがある) は過去の解決策に基づき一層具体化されたアイデアである。そして, 物理的効果 (約400)の知識ベースは, 物理・化学・幾何の効果の集成であって, 各効果が達成できる機能に従って索引づけされている。
SIT はいくつかの基本的な面でTRIZと異なる。対立の克服という概念は十分条件の適用によって置き換えられている。十分条件を通って問題を再定式化することが, 候補の解決策をテストするための明瞭に定義された明白な判断基準を作り出す。二つの方法のもう一つの重要な違いは, SIT が最小限の技法の組を使うことである。その結果, いくらかの訓練ののちには, 問題解決者にとって SITプロセスが第二の天性 [自然に出てくる力] になることができる。TRIZにおいては, 利用者はいつも膨大な外部データベースを参照しなければならない。
SIT が実験ベースで使われているのは, イスラエルのいくつかのハイテク企業と, 米国のフォード自動車会社 (Sickafus, 96) である。その方法はまた, 正規の学科として, テルアビブ大学(Tel-Aviv University) とシンガポール国立大学 (National University of Singapore) で教えられている。多数の創造的な解決策がSIT の実践者たちによって得られてきた。
2 節に技術的問題, ありきたりの解決策, および創造的解決策をセットにした例を示す。この例は十分条件に関する直感的な印象を形成するのに役立つ。ついで,
十分条件の形式的定義を 3節で与える。 4節では, 十分条件の実験的な研究を示す。
5節にSIT のメカニズムを記述する。SIT の適用のいくつかの例が 6節に示されている。
7節には結論と将来の研究計画を述べる。
2. 創造的解決策のための十分条件
十分条件を示すために, われわれはまず技術的問題の一つの例から始めよう。問題を解決するありきたりの解決策のいくつかとともに, 一つの創造的なアイデアが示されるだろう。これらのさまざまの解決策を簡単に分析することにより, 創造的なアイデアは, ありきたりのアイデアたちのどれとも共通でない, 特有の性質を持っていることが分かる。これらの性質はついで一般化され(なおかつ圧縮され),創造的解決策のための二つの(合わせて)十分条件の組に定式化されるであろう。
2.1 例 -- 材料テスト
ある会社が極めて過酷な環境条件に耐えることができる材料を開発している。耐久テストは容器の中で行われ, 試料は高温・高圧下で酸の液に浸けられる。問題は, 高温・高圧下で酸に曝されて, 容器がこの条件に耐えられず, しばしば取り替えなければならないことである。この例はAltshuller (85) から取ってきた。
ありきたりのアイデアたち: つぎに示すアイデアたちは,
上記の問題に遭遇した技術者たちが提案したもっとも普通のアイデアを集めたものである。
(a) 容器を保護材料の層でコートする。
(b) もう一つの少し小さな容器を現在の容器の中に設置する。中の容器はより安価な材料で作り,
ときどき取り替える。
(c) 酸の環境中で, より耐久性がある容器で,
現在の容器を置き換える。
一つの発明的解決策: テストする試料にドリルで穴を掘り, 酸をその穴に注ぐ。試料はついで [現在の] 容器中に置かれ必要な外部条件に設定される。酸は容器に接触しないから, だめになることもない。
解決策の分析: 発明的解決策は, どのありきたりの解決策にも共存していない二つの特有の性質を示す。第一の性質は, 新しい要素を加えられることがないことである。発明的解決策は既存のオブジェクトたち( すなわち, 容器, 酸, および試料) だけを用いている。
第二の性質は, 二つの変数の基本的な関係が質的に変化したことである。その変数は, 酸の濃度と, 容器を取り替えなければならない頻度とである。問題状態においては, 酸の濃度が高くなると, 容器はよりひどく損傷を受け, より頻繁に取り替えられる必要がある。それに対して, 解決策状態では, これら二つの変数には全く関係がない。容器と酸とはまったく接触しないので, 酸の濃度は無関係になる。
ありきたりの解決策のリストを調べると, それらの解決策のどれも, これら両方の性質を持たないことが分かる。第一の解決策は第一の性質を持たない。新しい要素, コーティング材料が追加されているからである。第二の解決策は両方の性質を持っていない。第三の解決策は第二の性質を満足しない。たとえ容器がより耐久性を持っても, そのダメージは (たとえ小さくても) やはり酸の濃度の関数であろう。
第一の性質は一般化されて, 閉世界(Closed World, CW)の条件になるであろう。一方, 第二の性質は問題の特性条件における定性的変化(Qualitative Change in Problem Characteristic Condition, QC)と呼ばれる。これら二つの条件を同時に満足するすべての解決策は, その分野の専門家たちによって創造的とみなされるであろうことを, 本理論は主張する。 4節には, これらの条件の充足と, 専門家による創造性の評価との間の関係を, 実験的な例証を掲げる。
3. 十分条件の形式的表現
本節では十分条件の形式的表現を与える。最初に表記法と定義を与え, ついでそれらを使って十分条件を定式化する。提案される表記法の体系は, ( 既知の) 望まない効果を被っている, 与えられた (既存の) 技術システムに関する用語で, 問題が記述されるという状況に対応している。
3.1 表記法と定義
Si 問題状態にある与えられたシステム (i はInput を表す)
So 解決策状態にあるシステム (o はoutputを表す)
N(S) システムS の近傍 ( そのシステムに組み込まれた部分ではないが, シス テムの近傍にあり, あるいは, そのシステムと特別な親近性をもつような オブジェクトの集合)
O(S) システムS を構成しているオブジェクトの型の集合。各オブジェクトは, システム中の機能を支えている一つの技術的概念を表す。
UDE (問題記述に現れている) 望まない効果 (undesired effects) に直接的あるいは間接的に寄与している変数の集合
f+(y, x) (他のすべての変数が不変であるとき) y はx の増加関数である。
f-(y, x) (他のすべての変数が不変であるとき) y はx の減少関数である。
f0(y, x) y の値はx の値に依存しない。
もし, x,y ∈ UDEのとき, f+(y,
x) は問題特性関数と呼ばれる。
これらの表記法と定義を用いると, 二つの十分条件はつぎのように表現される。
閉世界条件 (Closed World condition, CW condition):
O(So)
Y N(So) ⊆ O(Si) Y
N(Si)
(1)
問題特性の質的変化の条件 (Quality Change
in Problem Characteristic condition, QC condition):
x, y
∈ UDE に対して,
[f+(y,x)] Si ∧ [f0 (y,x) ∨ f-(y,x)]So
閉世界条件の式が意味することは, 新しいオブジェクトをシステムに追加することは (近傍のオブジェクトでない限り) できないが, システムからオブジェクトを除去することはできる。O(S)はオブジェクトの型を表していて, オブジェクトそのものではないので, 同じ型のもっと多くのオブジェクトをシステム中に導入することは許される (たとえば, 自動車にもっと多くの車輪を加えるなど) 。
問題特性の質的変化の条件の式は, 問題特性の一つが, 増加関数から, 減少関数または不変関数へと変わる必要があることを, 意味している。
十分条件は, 非常に多くの工学的問題と, それに対するありきたりの解決策/
創造的解決策を経験的に調査して, 開発された。条件がひとたび抽出されると,
それらの背後にある論理の説明を導き出すことができる。ふつう, ありきたりの設計問題解決のプロセスは,
パラメタを調節することから始まり, これが望ましい結果を出すことに失敗すると,
技術者たちは代替の技術コンセプトを探索することに向かう。QC条件はパラメタ調節を無効にし,
そしてCW条件が既存の概念を置き換えることを許さない。そこで, 問題解決者たちは,
もっと創造的なプロセスに頼るように強制される。
4. 創造性の評価と条件の充足との関係の経験的な例証
経験的テストの主要な目的は, これらの十分条件が創造性のための適切な条件であることを検証することである。経験的テストは, 創造性の評価と, ここで定義された十分条件とに正の関係があることを例証する。この研究のために, われわれは二つの予備段階を実施した。その第一は,関連のある工学的問題に対する解決策を,創造性の評点を用いて特徴づけるように設計された。第二段階を設計した意図は,やさしい課題については,解決策の評価に十分条件を適用することを,説明書きを用いて簡単にすんなりと教えることができる,ということを例証することであった。
これら二段階の結果が得られたので,第三の最終段階は,表1に示した二組のデータを統合することにより,達成することができた。一組のデータ(すなわち第一段階の結果) は創造性評点からなっている。つぎの組のデータ ( すなわち第二段階の結果) は条件の評価からなっている。
4.1 第一段階: 創造性の評価
被験者: 総計196 人の技術者(engineers) ( 内男性176 人, 女性20人) がこの研究に参加した。彼らの仕事の経験は 4年ないし20年に渡っている。
方法と手順: 各被験者に, (20 の問題群の中からランダムに選んだ) 一つの工学的問題と, 各問題についての3 〜10件の解決策の候補たちの記述とを, 提示する。その問題たちは, あらかじめ検査した50の工学的問題の集合の中からランダムに選ばれた標本であり, 各問題に対して [本件の二つの] 条件を満足する解決策が存在することが知られているものである。それらの問題は, 工学のさまざまの分野, たとえば, 機械工学, 電気工学, 土木工学など, から生じたものである。それらはいろいろな出典, たとえば, 特許文献, 産業界, および著者たち自身の経験など, から持ってきたものである。本件の50の問題の組は, 工学において普通に生じる問題の種類を代表しているものと, われわれは仮定している。解決策たちの各組は, 条件を満足する少なくとも一つの解決策とともに, 技術者たちから普通に提案される他の解決策たちを含んでいる。( これらの普通の解決策は, 著者たちが行った多数の創造的問題解決ワークショップにおいて集めてきたものてある) 。いろいろな解決策は被験者にランダムな順番で提示された。被験者たちは, 各解決策をその発明性の度合いによって, 1 ( 全く発明的でない) から 7 (非常に発明的である) までのスケールでランクづけするように依頼された。
4.2 第二段階: 十分条件の評価
被験者たち: 被験者たちは, テルアビブ大学においてより高い学位を目指して勉学している20名の学生たちの中からランダムに選んだ, 3名の技術者である。この実験のために 3名の被験者を選んだのは, 無作為分布の厳密に統計的な性質を目指したものではなく, 単に被験者の評価を相互チェックできるようにするためである。原理的に, 一つの解決策が条件を満たしているかどうかを評価するプロセスは, ( いくらかの誤差の余地を残す必要があるにしても) 決定論的なプロセスである。
方法と手順: この実験で審判者として働く被験者たちに, 十分条件をテストする手順を記述した20頁の小冊子が渡された。ついで, 被験者たちには, 第一段階の実験で使われた, 20の問題群とそれらの解決策の組が, 共通に渡された。各解決策が, CW条件およびQC条件を満たしているかどうかをテストするように, 被験者たちは求められた。もし審判者の過半数が両条件を満たしているとみなすと, その解決策は「審判者の観点から両条件を満たしている」ものと見なされる。第二段階の結果は, 表1 中に散らばっている「J 」記号で表されている。
4.3 第一・第二段階の結果の統合
表1 が第一段階および第二段階の結果を統合して示している。各行が異なる問題を示していて,
各行のひとつひとつのセルが解決策の候補を表す。各セルはその解決策の平均評価点を表す一つの数字を含んでおり,
また, オプションとして記号「* 」および「J 」が付加されている。「*
」はその解決策が両条件を満たしているものと著者たちがみなしていること, また,
「J」は同様に審判者たちがみなしていることを, それぞれ表す。各行では,
読みやすくするために, 解決策たちを (第一段階の) 創造性評価の評価点が高いものから低いものへの順に並べてある。
表1. 実験1 および実験2 の結果
| 問題番号 | 応答数 | 解決策1 | 解決策2 | 解決策3 | 解決策4 | 解決策5 | 解決策6 | 解決策7 |
| 1 | 9 | 5.1*J | 4.5J | 4.0 | 2.7 | 2.5 | 2.3 | 1.7 |
| 2 | 11 | 6.4*J | 5.0 | 4.9J | 4.9 | 4.6 | 3.8 | 3.8 |
| 3 | 11 | 5.9*J | 4.8J | 3.6 | 3.0 | 2.4 | ||
| 4 | 9 | 5.6*J | 4 | 3.2 | 2.6 | 2.4 | ||
| 5 | 9 | 5.1*J | 4.4*J | 2.9 | 1.6 | |||
| 6 | 10 | 5.4*J | 3.7 | 3.1 | 3.0J | 2.4 | 1.3 | |
| 7 | 10 | 6.0*J | 5.5 | 4.8*J | 4.1J | 3.9 | 3.1 | |
| 8 | 11 | 5.7*J | 5.3J | 5.2*J | 3.1J | 3.0 | 1.7 | 1.5 |
| 9 | 10 | 6.5*J | 2.8 | 2.3 | 1.8 | |||
| 10 | 12 | 4.8*J | 4.8*J | 4.1*J | 3.6 | 3.2 | 2.7 | |
| 11 | 10 | 5.3*J | 4.8*J | 3.0 | 3.0 | 2.8 | 2.6 | |
| 12 | 9 | 5.9*J | 5.4 | 2.9 | 1.7 | |||
| 13 | 9 | 4.8*J | 3.8J | 1.8 | ||||
| 14 | 9 | 6.2*J | 5.7*J | 4.3 | 2.0 | |||
| 15 | 12 | 5.2 | 4.2*J | 1.6 | ||||
| 16 | 9 | 6.4*J | 4.9 | 2.1 | ||||
| 17 | 10 | 5.6*J | 5.0J | 3.5 | 3.4 | |||
| 18 | 9 | 5.5*J | 5.3*J | 3.2 | 2.5 | 2.3 | 2.2 | |
| 19 | 9 | 5.8*J | 3.7* | 3.5*J | 2.5 | 1.5 | ||
| 20 | 9 | 6.1*J | 5.1*J | 5.1 | 1.7 |
4.4 結果の分析 --直接的観察
表1 をざっと見て分かるのは, 問題15以外のすべてのケースで, 両条件を満足する解決策が最高の創造性評価点を得ていることである。問題6, 8, 13および19以外のすべての問題で, 両条件を満たしている解決策たちは 4以上の評価点を得ている。しかし, 問題6,8,および13において, 低い評価を得たそれらの解決策たちについて, 著者たちは両条件を満足していると判断していない。
審判者たちの結果は, 90% 以上のケースについて, 著者たちの結果と一致している。また, 特定の解決策で「* 」ではないが「J 」と判定されたケースに関しても, その大部分のケースで, その解決策は創造性評価において比較的高い評価点を得ていることは, 注目に値する。本件の十分条件が解釈による誤差にあまり敏感でないという事実を, このことは例証している。
4.5 結果の分析 -- 点双列相関係数
点双列相関検定 (Point-biserial correlation
test)を, 二値の非数値変数 (ダミー変数と呼ばれる) と数値連続変数との間の相関を計算するのに,
用いた。二値のダミー変数 (両条件を満たさないとき 0で, 満たすとき1 の値を取る)
と, 創造性評価点との間の, 点双列相関係数を計算した。0.7 という値が得られた。この値が意味するのは,
創造性の評価点の分散の49% が, 解決策が両条件を満たすか満たさないかによって説明できる,
ということである。これは, この種の実験 (人間の判断を含む実験) においては非常に高いスコアと見なされる。これらの
(一つの変数に対する) 二つの値によって, [ 評価点の]
変動の非常に大きな部分をが明確となることを意味する。図1 は, この両条件との関連で
[充足している/ していないに分けて] 創造性の評価点をグラフに示したものである。
 |
|
| . |
図1. 十分条件との関連で見た創造性の評価点 |
5. SIT 法の記述
SIT 法 (SIT Mechanism)は三つの主要ステップで構成される。十分条件による問題の再定式化, 一般的思考戦略の選択, および, 関連するアイデア生成技法の選択と適用, という三ステップである。以下に各ステップを少し詳しく述べる。SIT 法についてのより形式的な説明は(Horowitz and Maimon, 97) にある。
5.1 問題の再定式化
この段階において, 問題解決者は, 問題解決の課題の目標を二つの十分条件を用いて設定する。CW条件が現在の制約に追加され, 一方, QC条件が目標を変更する。望ましくない効果のレベルを下げようという, 初期の( そして自然な) 要求の代わりに, 問題の任意の二つの関連する変数( 問題特性) の間の数学的関係に対して, 定性的変化を見いだすように, 問題解決者は導かれる。
この段階でユーザが技術的に作成するのは, システムのオブジェクトたちのリスト, システム近傍のオブジェクトたちのリスト, および問題特性変数のリストである。問題解決の課題はつぎのように定義される。すなわち, ひとつの解決策で, 定義された増加関数のうちの少なくとも一つが, 減少または不変関数になるように, ただし, その解決策が与えられたシステムおよびその近傍の要素で関与するリストの中に現れているものだけを組み込むという制約条件に従うものを, 見いだせ。
5.2 戦略の選択
十分条件による枠組みは, 自然に, 二つの思考戦略を生じさせる。候補解決策は, 三つの要素から構成される。すなわち, (QC 条件から導出される) 望ましい物理的目標状態, 修正されるべきオブジェクトたち, そして, 必要な修正である。CW条件は修正されるべきオブジェクトたちを既存のものだけに制約するので, その結果として, 探索空間をはっきりと狭める。二つのシナリオがこの段階で可能である。
1. 問題解決者が, QC条件から必要とされる物理的目標状態を導くことができる。望ましい目標状態がある単純な物理的操作によって達成でき, その操作がシステムが必要とする他の操作と相互干渉しないような場合に, この状況が普通に起こる。
2. 問題解決者が, 望ましい物理的目標状態を想起することができない, あるいは, 彼が考えることができる状態が, システムからの他の基本的な要求と矛盾する。
これらの二つのシナリオが二つの戦略候補 (possible strategies)を定義する。第一の戦略に従うと, 問題解決者は最初に概念的解決策を定式化する。それは一つの単純な操作であって, それがシステムに加えられると, QC条件が満たされることが保証されている。それから彼は, その望ましい操作を実行するオブジェクトを既存のものの中から見いだすことに進む。たとえば, [2節で扱った] 試料検査の問題を解決する過程において, 問題解決者は酸の液体と容器とを物理的に分離するというアイデアを思いつくことができる。それはQC条件をみたすことが保証されている一つのアイデアである。彼はそれから一つの既存のオブジェクトを選択する。この操作を実行するために, 検査される試料を選択したのである。この戦略は「拡張戦略」と呼ばれる。それは, 新しい操作を実行する仮想的なオブジェクトを追加することにより, システムが一時的に拡張されるという事実を示すためである。
もし, この段階で問題解決者が第二の状況に達したとき, すなわち, QC条件を満足することを保証する望ましい目標状態を考えつくことができない場合には, 彼は異なる戦略に従うことができる。すなわち, 試行錯誤のプロセスによって, 既存のオブジェクトたちに対してさまざまの可能な修正を試み, ついにはなんらかの時点で, QC条件を満足する状態にぶつかると期待される( ここで, CW条件は満足することが保証されている。なぜなら, 試行する修正のどれもその条件を侵害しないからである) 。この戦略は「再構築戦略」と呼ばれる。それは, 試行錯誤のプロセスにおいて, 問題解決者は既存オブジェクトたちとその組織の構造を変える事実を明示するためである。
問題分析者は, もし彼が概念的解決策を考えつくことができれば, 拡張戦略を選択し, そうでなければ, 再構築戦略を選択するように導かれる。思考の戦略を選択することの実際の意義は, それぞれの戦略に対して, アイデア生成技法の異なる組を適用することにある。拡張戦略が選択された場合には, ユーザは統合化(unification) または乗算 (multiplication)のどちらかの方法を適用するように導かれる。他方, 再構築戦略が選択された場合には, ユーザは除算(division)または可変性の増加(increasing variability)のどちらかの方法を適用するように導かれる。拡張技法たち [すなわち, 統合化と乗算] は, 問題解決者が新しい操作を実行できる既存のオブジェクトを同定することを助け, 一方, 再構築技法 [すなわち, 除算と可変性の増加] は, 彼がシステムの可能な変更についての自由度を増すことを助ける。
5.3 アイデア生成技法
アイデア生成は本方法の最終段階である。 [アイデア生成技法の] 主要な役割は問題解決者を凝り固まった心理状態から自由にすることである。
5.3.1 統合化技法 (The Unification Technique)
統合化技法は, 問題解決者が, 概念的解決策で定義された操作を実行するような, システムまたは近傍オブジェクトを同定することを助ける。この方法を適用するには, つぎの4 段階のプロセスを経る。
(1) 必要な操作を定式化する。
(2) 主システムおよび近傍のすべてのオブジェクトのリストを作る。
(3) リストから一つのオブジェクトを選び,
つぎの文を完成させる。「<選択されたオブジェクト>がその<操作>を実行する」
(4) 選択したオブジェクトに必要な修正を決定し,
望ましい操作が実行できるようにする。
例: 試料テスト問題に上記の 4ステップを適用したもの:
(1) 必要な操作:
酸の液を容器から分離する。
(2) オブジェクトのリスト:
容器, 試料たち, 酸の液
(3) 選択したオブジェクト:
試料。「試料が酸の液を容器から分離する」
(4) 必要な修正:
試料の形状を変えて, 試料が液を入れることができるようにする。
5.3.2 乗算法 (The Multiplication Technique)
この技法の目的, および, その(4ステップのうちの) 最初の二つのステップは, 上記の統合化法と同じである。後半の二つのステップをつぎに示す。
(3) リストから一つのオブジェクトを選択して, つぎの文を完成させる。「<選択されたオブジェクト>は乗算[複数化]される。<このオブジェクト>の新しいコピー(またはコピーたち)が,<必要な操作>を行う。」
(4) 選択されたオブジェクトの新しいコピー (またはコピーたち) に対する必要な修正を決定し, 望ましい操作を実行できるようにする。
5.3.3 除算法 (The Division Tecnique)
除算法は再構築戦略技法の一つであり, その目的は, ユーザがシステムのオブジェクトを修正し再組織化するための新しい自由度を同定することを助ける。つぎのような 3ステップのプロセスである。
(1) システムのオブジェクトのリストを作る。
(2) リストから一つのオブジェクトを選択し, つぎの文を完成させる。「<そのオブジェクト>を,そのもっと基礎的な要素に/同じ部分からなるより小さな部分たちに/ランダムなやり方で,分割する。」(注:これらの三つの選択枝から一つを選ぶ。)
(3) 意味を探索する。[上記で得られた] 新しい自由度を使って, QC条件が満たされる状態を創造するように試みる。さまざまの部分をさまざまの位置に置く, 部分の順番をさまざまに試みる, など。
5.3.4 可変性の増加の技法 (The Increasing Variability Technique)
問題解決者が問題を解決するための新しい自由度と新しい方法を創造することを支援する, もう一つの重要な技法である。つぎのような 4ステップのプロセスである。
(1) システムのオブジェクトたちのリストを作る。
(2) 一つのオブジェクトを選択する。
(3) 現在は関係を持たない
(すなわち, 関数関係にない) 二つのパラメタW とZ を選択する。( 新しい自由度は,
両者の関係の型となる。)
(4) 意味を探索する。新しい自由度を用いて,
QC条件を満足する状態を創造することを試みる。
6. SIT法の応用例
本節では, 技術的問題に対する創造的解決策を見いだすのに, どのようにSIT 法を使うかを例示する。各例はつぎのものを記述する: 問題の記述, ありきたりの解決策の組 (技術者たちからの最も普通の反応), 問題解決にどのようにSIT 法を使うかの詳細な記述, および創造的解決策 (SIT プロセスの出力) の記述。ふつうのSIT 法の適用では, 多くの試行錯誤がある (異なる戦略, 異なる技法, 技法の異なる適用など) ことに注意しておくことが重要である。しかし, 以下の記述ではSIT 法の応用のこの重要な性質を反映していない。簡潔さのために, 各例において, 解決策への直接のパスだけを記述している。
6.1 例題1 -- パイプの中のとうもろこし
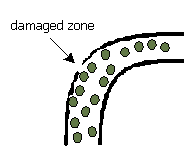
曲がった鋼鉄のパイプが, とうもろこし処理工場の部品の一部である。パイプの機能は空気流でとうもろこしの粒を移送することである。問題は,
曲がった部分のパイプに対する粒の衝撃であり, このためにパイプ壁が磨耗する。空気の流速を下げることはできない,
それは工場の処理性能を下げるからである。この問題は最初にAltshuller (85)
に現れた。
 |
|
| . |
図2. パイプの中のとうもろこしの問題 |
6.1.1 ありきたりのアイデアたち:
(a) 磨耗領域でパイプを強化する
(材料を変える, 分厚くする, など)
(b) パイプの湾曲部分を別の小片で作り,
容易に取り替えができるようにする。
(c) パイプを保護層でコーティングし,
その保護層をときどき取り替える。
6.1.2 SIT法 ステップ1 -- 問題の再定式化:
UDE パラメタのリスト: 製造コスト, 磨耗速度, 穀物粒の流れ, 穀物の硬さ
システムおよび近傍のオブジェクトのリスト: パイプ, 穀物粒, 空気流
再定式化した問題: 磨耗速度を, 穀物粒の流れに関し無関係/ 減少関数にせよ。ただし, パイプ, 穀物, および空気流の他には, 新しいオブジェクトを追加してはならない。
6.1.3 SIT法ステップ2-- 戦略の選択
概念的解決策が着想された( 「穀物粒をパイプから分離する」) ので, 拡張戦略を選択する。
6.1.4 SIT 法ステップ3 --アイデア生成技法 (統合化または複数化) を選択・適用
統合化法 (Unification)を選択した。技法の適用:
(1) 必要な操作の定式化:
穀物粒をパイプから分離する。
(2) 主システムおよび近傍のすべてのオブジェクトのリストを作る:
穀物粒, パイプ, 空気流
(3) リストから一つのオブジェクトを選択:
穀物粒を選択
つぎの文を完成させる:
「<穀物粒>が<穀物粒をパイプから分離する>を実行する。」
(4) 選択したオブジェクトの必要な修正を決定し,望ましい操作を実行できるようにする: 穀物粒がパイプの湾曲した部分にくっつくべきである。
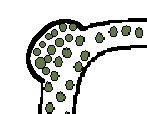
6.1.5 解決策
パイプの湾曲した領域の幾何学的形状を変化させ,
ポケットを作って, 穀物粒たちがそこにたまることができるようにする。これによって,
パイプは穀物粒の衝撃による損傷から保護される。( 図3 参照)
 |
|
| . |
図3. パイプの中のとうもろこしの問題に対する解決策 |
6.2 例題2: 脱線検知器
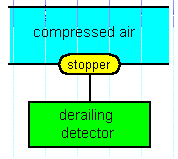
列車のブレーキシステムは, 列車と平行に走る一つのパイプを含んでいて, パイプ内の空気は 5気圧にしてある。この圧力が落ちると, 列車は停止する。非常の場合 (たとえば脱線時) には, この空気が非常に速く放出されなければならない。空気を十分速く放出するためには, 少なくとも10cm2 の大きさの出口から出なければならない。通常の運転条件では, この口は栓 (ストッパー) で塞がれていなければならない。この栓は空気圧そのもので解放されるべきである。
新しい脱線検知器が開発されている。そのアイデアは,
正常運転時には, 栓は脱線検知器によって正規の状態に保持され, そして, 脱線が起こったときには,
検知器は栓に対して力を及ぼすことを止め, 栓が開放される, というものである。問題なのは,
脱線検知器は0.5 Kg重の力しか出すことができず, 内圧で掛かっている50Kg重の力とバランスするのに不十分なことである。
 |
|
| . |
図4. 脱線検出システム |
6.2.1 ありきたりのアイデア:
(a) てこを使う。
(b) 脱線検出器の数を増やす。各々の検出器は小さな栓を支持する。
(c) 栓をねじ込んで設置しておく。摩擦が負荷のいくらかを担う。
6.2.2 SIT法ステップ1 --問題の再定式化
UDE パラメタのリスト: 誤って警報をする確率, 予期せずに栓が開く確率, 脱線検出器への負荷, 空気の圧力, 栓の断面積
システムおよび近傍のオブジェクトのリスト: パイプ, 空気, 栓, 脱線検出器
再定式化した問題: 脱線検出器への負荷を, 空気圧力に対して不変または減少関数にせよ。ただし, つぎのものの他に新しいオブジェクトを追加してはならない: パイプ, 空気, 栓, 脱線検出器
6.2.3 SIT法ステップ2 --戦略の選択
概念的解決策は考えついた。「栓に対して, 空気圧が及ぼしている力と大きさが同じで向きが反対の力をかける。」よって, 拡張戦略を採用した。
6.2.4 SIT 法ステップ3 --アイデア生成技法 (統合化法または乗算法) を選択・適用
乗算法を選択した。技法の適用:
(1) 必要な操作を定式化する:
栓に対して, 空気圧が及ぼしている力と大きさが同じで向きが反対の力をかける。
(2) 主システムおよび近傍のすべてのオブジェクトのリストを作成する:
パイプ,
空気, 栓, 脱線検出器
(3) リストから一つのオブジェクトを選択し,
つぎの文を完成させる: <栓>を選択。<栓>が複数化される。このオブジェクトのコピー(またはコピーたち)が<栓に対して,
空気圧が及ぼしている力と大きさが同じで向きが反対の力をかける>。
(4) 選択されたオブジェクトの新しいコピー
(またはコピーたち) に対する必要な修正を決定し, 望ましい操作を実行できるようにする:
新しい栓はもとの栓よりも少し小さくし,
脱線検出器がいくらかの負荷を分担するようにする。
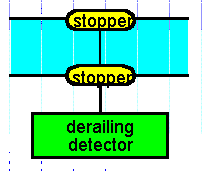
6.2.5 解決策:
新しい栓はもとの栓のすぐ上に装着し, 両者を細い針金で連結する。(
図5 参照)
 |
|
| . |
図5. 脱線検出器問題の解決策 |
6.3 例題3 --腫瘍問題
あなたは医者で, 胃に悪性の手術不可能な腫瘍を持っている患者に直面していると考えなさい。腫瘍を壊さないと, 患者は死ぬだろう。腫瘍を壊すのに使うことができる光線がある。もしその光線を十分な強度で腫瘍に当てると, 腫瘍は破壊される。しかし, 不幸にも, この強度では, 光線は腫瘍に向かうときに通過する健康な組織をも破壊するだろう。より弱い強度では, 光線は健康な組織にとって無害であるが, 腫瘍にも作用を及ぼさない。
6.3.1 ありきたりのアイデア:
この問題では, 普通の大部分のアイデアは, 問題定義に違反している (たとえば, 問題文が腫瘍は手術不可能であると明確に言っているにもかかわらず手術をしようとする, など) か, あるいは, 化学療法のような別の処置を提案する。
6.3.2 SIT法ステップ1 --問題の再定式化
UDE パラメタのリスト: 患者の死の確率, 健康な組織の損傷, 光線強度
システムと近傍のオブジェクトのリスト: 光線, 腫瘍, 健康な組織
再定式化された問題: 健康な組織の損傷を, 光線強度に対して, 不変化または減少関数にせよ。ただし, つぎのオブジェクトリストに新しいオブジェクトを追加してはならない: 光線, 腫瘍, 健康な組織
6.3.3 SIT法ステップ2 --戦略の選択
概念的解決策を考えることができないので, 再構築戦略を選択する。
6.3.4 SIT法ステップ3 --アイデア生成技法( 除算法または可変性の増加法) を選択・適用
除算法を選択した。技法の適用:
(1) システムのオブジェクトのリストを作成する:
光線 (これが唯一のシステムオブジェクトである)
(2) リストから一つのオブジェクトを選択し,
つぎの文を完成させる:
<光線>を選択した。<光線>が<同じ型のより小さな部分に>分割される。
(3) 意味を探索する。[上記で得られた]
新しい自由度を使って, QC条件が満たされる状態を創造するように試みる( さまざまの部分をさまざまの位置に置く,
部分の順番をさまざまに試みる, など) : より小さな光線たちは, さまざまな角度から腫瘍に向けられる。
6.3.5 解決策
少数の弱い光線を異なる角度から腫瘍に向けて投じ, 腫瘍のところで収束し, そこで十分な強度になって, 腫瘍を破壊するようにする。QC条件は満足されている。なぜなら, 弱い光線の数を増すことによって, 光線が通過する健康な組織に害を与えずに, 腫瘍の位置での光線強度を増大させることができるからである。
6.4 例題4 -- 固体燃料ロケットエンジン
固体燃料のロケットエンジンの技術者たちが直面していた問題の一つは,
エンジンからの推進力を一定にすることを達成する必要があった。固体燃料ロケットエンジンは,
空洞の筒の形をして, その内部の囲みで燃焼する。そのような形状に伴う問題は,
内部の囲みの面積の変化 (半径が増加するから) のために推進力が一定でないことであった。内部の燃焼領域が増加するにつれて,
推進力が増加する。
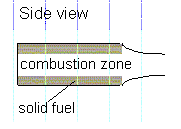 |
|
| . |
図6. ロケットエンジンの側面断面図 |
6.4.1 ありきたりのアイデア
(a) 新しいパラメータの設計 (a
new parametric design): 筒の寸法を変えて, より長く, より細くする。この変更でも総体積と燃焼面積は維持され,
初期と最終の半径の差が小さいので, [ 推進力の] 変化がより小さくなる。
(b) 「タバコの燃焼」--筒の底が燃焼する。
6.4.2 SIT法ステップ1 --問題の再定式化
UDE パラメータのリスト: エネルギーの浪費, 均一でない推進力, 燃焼面積の増加, 周の増加
システムおよび近傍のオブジェクトたちのリスト: 固体燃料, ロケット, 推進力
再定式化された問題: 燃焼面積を, 周の不変化または減少関数にする, ただし, つぎのオブジェクトのリストに新しいオブジェクトを追加してはならない: 固体燃料, ロケット, 推進力
6.4.3 SIT法ステップ2 --戦略の選択
概念的解決策を考えつことができないので, 再構築戦略を選択した。
6.4.4 SIT法ステップ3 --アイデア生成技法( 除算法または可変性の増加法) を選択・適用
可変性の増加法を選択した。技法の適用:
(1) システムのオブジェクトのリストを作成する:
固体燃料,
ロケット, 推進力
(2) リストから一つのオブジェクトを選択する:
固体燃料
(3) 現在は関係を持たない (すなわち,
関数関係にない) 二つのパラメタW とZ を選択する。( 新しい自由度は, 両者の関係の型となる。):
Z として 断面積の形, W として燃焼の進行を選んだ。
(4) 意味を探索する。新しい自由度を用いて,
QC条件を満足する状態を創造することを試みる : 断面積の形が燃焼の進行とともに変化する。最初は複雑な曲がりくねった形で,
最後は単純な円形。
6.4.5 解決策
断面の形状を燃焼の進行の間一定の周を保つようにする。断面は複雑な形から単純な円に変化し,
その結果, 平均半径は増大するけれども, 周は一定に留まる。図7 がそのアイデアを例示する。この解決策は,
内部の囲みで燃焼する空洞の形状という初期の概念を保存しており, その結果,
閉世界条件に従っている。推進力の変化はいつもゼロであるから, 初期および最終の半径の違いに全く無関係であり,
解決策はQC条件をも満足している。注目すべきことは, この解決策が, その当時,
固体燃料ロケットにおけるブレークスルーであったことである。われわれのワークショップにおいては,
研修生たちが, 十分条件を用いてこの解決策を全く素早く見つけるのを見てきた。
 |
|
| . |
図7. 燃焼の進行に伴う新しい内面の形状 |
7. 結論および将来の研究の計画
本論文は創造的解決策のための客観的な十分条件の組, および, これらの条件を満足する解決策に向けて探索を構造化した三段階の方法を提示した。十分条件を特定の問題に適用すると, 与えられた問題の定義が修正される。すなわち, QC条件が探索の目標を変え, CW条件が探索空間を限定する。十分条件を適用することにより, 創造的な問題解決者は, その非創造的な仲間たちとは, 実際上異なる問題を解く。これは異なる解決策, ときとして驚くべき解決策を見つける重要な因子となる。
十分条件の有用性は 4節に提示した経験的な研究を通じて示された。両条件を満足する解決策は, 分野の専門家たちの創造性評価において高い点数を獲得したことが示された。工学的問題を創造的に解くのにSIT が有効であることを, 経験的に示すことを目指して, われわれはいま研究を進めているところである。われわれはまた, Kreitler and Kreitler (69)が開発した個人意味プロファイルアセスメント (individual meaning profile assesssment) を用いて, SIT 法の研修者の内面のより深い認知的な変化を研究している。
中間的な結果が示しているのは, 被験者たちが工学的問題を創造的に解く能力が, 顕著に改良されたことである。両条件を満足する解決策を見つけるのに成功する人たちの割合は, 研修前の平均8%から, 研修後の30% 以上へと増大している。SIT 法の研修の前と後で, 認知スタイルにいくつかの興味深い変化があることが, 認知テストの結果分かってきている。
7.1 SIT 法とTRIZとの主要な差異
いまやSIT 法を明らかにしたので, SIT 法とその先駆であるTRIZとの主要な違いを要約しておこう。
(a) SIT 法は最小限の組の技法を使う: 5個のアイデア生成技法。 一方, TRIZでは何百という技法が使われる。このSIT 法の特徴は望ましい解決策への道筋を短くする。
(b) SIT 法は, 問題解決者を, 真に創造的なアイデアの枠組み中に保つ点で, より強く束縛している(tighter)。この理由は十分条件にある。閉世界(CW)条件および問題特性の定性的変化(QC)の条件は, TRIZにおける「矛盾の克服」という要請を置き換えるものであり, 候補となるアイデアにテスト容易な要求を課する。TRIZの文献は多数の教育的な解決策を載せており, それらはそれぞれ矛盾を解消したものであるといわれているが, 本件の十分条件を満足していないものもある。
(c) SIT 法のトレーニングはTRIZのトレーニングと異なる。SIT 法の簡潔ですっきりとした構造のために, SIT 法の研修者は同じ技法をさまざまな問題に対して繰り返し練習し, ついにはそれらがかれの第二の天性となる。実生活でこの方法を使うときには, 問題解決者はいかなる外部知識ベースをも参照せず, 彼自身の長期記憶からこれらのツールを引き出して使う。
これらの違いにもかかわらず, 両者のアプローチは相補的である。ときには, TRIZで示唆されているように, 解決策の原理の大きなデータベースを探索することが有用であろう。しかしながら, SIT 法のトレーニングは, TRIZのアイデアバンクから意味を引き出すように, 各人を訓練する優れた方法である。
7.2 将来の研究
将来, われわれは, SIT 法の学習, 練習, 応用,
および共同作業を支援するような計算機環境を開発することを意図している。そのシステムはまた,
過去の創造的解決策の事例のデータベースを作成・維持することを支援するであろう。これは,
解決策だけでなく, 解決策に導いたプロセス (袋小路も含めて) をも記憶する。構造化された解決策プロセスのデータベースは,
組織にとって重要な資産となるであろう。
文献
Allen M. S., Morphological
Creativity, Prentice-Hall, New Jersey, 1962.
Altshuller
G. S., Creativity as an Exact Science, Gordon and Breach, New York,1985.
Dasgupta, S.,
Creativity
in Invention and Design, Cambridge University Press, 1994.
de Bono E., Serious
Creativity, Fontana, 1992.
Fey R., E.I.
Rivin,
Vertkin
I.M., "Application of the Theory of Inventive Problem Solving to Design
and Manufacturing Systems", Annals of the CIRP, 43, January, 1994.
Gordon W.J.,
Synectics,
Harper and Brothers, New York, 1961.
Honnessey A.
and Amabile T. M., "The conditions of Creativith",
in the Nature of Creativity, Robert J. Sterenberg (ed.), pp. 11-38,
Cambrisge University Press, 1988.
Horowitz R.,
Maimon
O., "SIT (Structured Inventive Thinking)- A Method for Enhancing Creative
Problem Solving in Engineering", submitted for publication in IEEE Systems
Man and Cybernetics, 1997.
Kreitler H,
Kreitler S., "Dimensions of Meaning and Their Measurement", Psychological
Reports 23, pp. 1307-1329, 1968.
Maimon, O., Horowitz,
R. "Sufficient Conditions for Design Inventions", submitted for publication
in IEEE Systems Man and Cybernetics.
Malmqvist J.,
Axelsson
R., Johansson M., "A Comparative Analysis
of the Theory of Inventive Problem Solving and the Systematic Approach
of Pahl and Beitz", Proceedings of the 1996 ASME Design Engineering Technical
Conference, 1996.
Osborn, A. F.,
Applied Imagination, New York: Charles Scribner's Sons, 1959.
Sickafus E. N.,
"Structured Inventive Thinking", The Industrial Physicist, March 1996.
Sushkov V., Mars
N. J., Wognum P. M., "Introduction to TIPS:
a theory for creative design", Artificial Intelligence in Engineering,
9, 1995.
| 本ページの先頭 | 論文の先頭 | 2. 十分条件 | 4. 経験的実証 | 5. SIT法のプロセス | 6. SIT法の適用例 |
| 本ページの先頭 | Sickafus USIT法第2論文 (99.03) | 中川 USITセミナー(2) | English
page |
| ホームページ | 論文・技術報告集 | TRIZフォーラム |
最終更新日 : 2000. 3.23. 連絡先: 中川 徹 nakagawa@utc.osaka-gu.ac.jp